Login

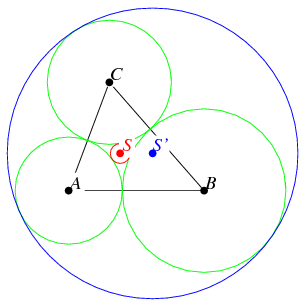
 Give ideas to make a PPT on Heron's formula and Triangle and its angles.Please i will br really vey very obliged to you.

 Triangle and its angle :-

Triangles

A triangle has three sides and three angles 

The three angles always add to 180°

Equilateral, Isosceles and Scalene

There are three special names given to triangles that tell how many sides (or angles) are equal.

There can be 3, 2 or no equal sides/angles:

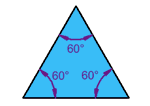Equilateral Triangle

Equilateral Triangle

Three equal sides 
Three equal angles, always 60°

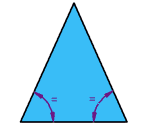Isosceles Triangle

Isosceles Triangle

Two equal sides 
Two equal angles

Scalene Triangle

Scalene Triangle

No equal sides 
No equal angles

What Type of Angle?

Triangles can also have names that tell you what type of angle is inside:

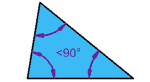Acute Triangle

Acute Triangle

All angles are less than 90°

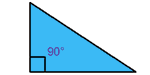Right Triangle

Right Triangle

Has a right angle (90°)

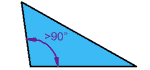Obtuse Triangle

Obtuse Triangle

Has an angle more than 90°

Combining the Names

Sometimes a triangle will have two names, for example:

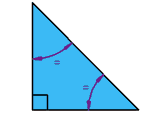Right Isosceles Triangle

Right Isosceles Triangle

Has a right angle (90°), and also two equal angles

Can you guess what the equal angles are?

  • 2
View Full Answer

 Hii,

In, Power Point Presentation, You can show how the Heron' formula was derived or maybe you can prove it ! 
In my opinion the best is to explain it.... i.e what exactly it is ! 

Like this -> 

Heron's Formula

An important theorem in plane geometry, also known as Hero's formula. Given the lengths of the sides a, b, and cand the semiperimeter

s=1/2(a+b+c)
(1)

of a triangle, Heron's formula gives the area Delta of the triangle as

Delta=sqrt(s(s-a)(s-b)(s-c)).
(2)

Heron's formula may be stated beautifully using a Cayley-Menger determinant as

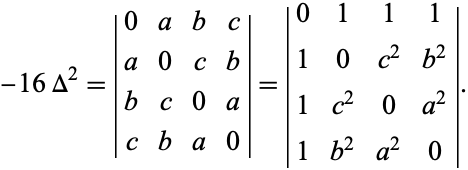
-16Delta^2=|0 a b c; a 0 c b; b c 0 a; c b a 0|=|0 1 1 1; 1 0 c^2 b^2; 1 c^2 0 a^2; 1 b^2 a^2 0|.
(3)

Another highly symmetrical form is given by

(4Delta)^2=[a^2 b^2 c^2][-1 1 1; 1 -1 1; 1 1 -1][a^2; b^2; c^2]
(4)

(Buchholz 1992).

SoddyCircles

Expressing the side lengths a, b, and c in terms of the radii a^', b^', and c' of the mutually tangent circles centered on the triangle vertices (which define the Soddy circles),

a=b^'+c^'
(5)
b=a^'+c^'
(6)
c=a^'+b^',
(7)

gives the particularly pretty form

Delta=sqrt(a^'b^'c^'(a^'+b^'+c^')).
(8)

Heron's proof (Dunham 1990) is ingenious but extremely convoluted, bringing together a sequence of apparently unrelated geometric identities and relying on the properties of cyclic quadrilaterals and right triangles. Heron's proof can be found in Proposition 1.8 of his work Metrica (ca. 100 BC-100 AD). This manuscript had been lost for centuries until a fragment was discovered in 1894 and a complete copy in 1896 (Dunham 1990, p. 118). More recently, writings of the Arab scholar Abu'l Raihan Muhammed al-Biruni have credited the formula to Heron's predecessor Archimedes prior to 212 BC (van der Waerden 1961, pp. 228 and 277; Coxeter and Greitzer 1967, p. 59; Kline 1990; Bell 1986, p. 58; Dunham 1990, p. 127).

A much more accessible algebraic proof proceeds from the law of cosines,

cosA=(b^2+c^2-a^2)/(2bc).
(9)

Then

sinA=(sqrt(-a^4-b^4-c^4+2b^2c^2+2c^2a^2+2a^2b^2))/(2bc),
(10)

giving

Delta=1/2bcsinA
(11)
=1/4sqrt(2(b^2c^2+c^2a^2+a^2b^2)-(a^4+b^4+c^4))
(12)
=1/4sqrt((2ab)^2-(a^2+b^2-c^2)^2)
(13)
=1/4sqrt((a+b+c)(-a+b+c)(a-b+c)(a+b-c))
(14)
=sqrt(s(s-a)(s-b)(s-c))
(15)
 

 

  • 0

Hope this helps ! :)

  • 0
What are you looking for?